Unit 1: Real Numbers
Class 9 Mathematics | Punjab Curriculum and Textbook Board Syllabus 2025
1. Define rational numbers.
The number of the form \( \frac{p}{q} \) where \( p,q \) are integers and \( q \neq 0 \) are called rational numbers.
Examples: \( \frac{2}{9}, \quad 7, \quad \sqrt{\frac{25}{16}} \)
\( Q = \left\{ x|x = \frac{p}{q}, \quad p,q \in \mathbb{Z} \land q \neq 0 \right\} \)
2. Define irrational numbers.
The number which cannot be expressed in the form \( \frac{p}{q} \) where \( p,q \) are integers and \( q \neq 0 \) are called irrational numbers.
Examples: \( e, \quad \pi, \quad \sqrt{2} \)
\( Q' = \left\{ x|x \neq \frac{p}{q}, \quad p,q \in \mathbb{Z} \land q \neq 0 \right\} \)
3. Define set of real numbers.
The union of the set of rational numbers and irrational numbers is known as the set of real numbers. It is denoted by \( \mathbb{R} \).
\( \mathbb{R} = Q \cup Q' \)
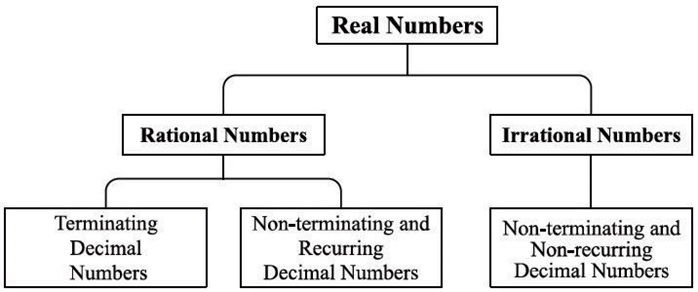
4. Explain decimal representation of rational numbers.
The decimal representations of rational numbers are of two types:
-
Terminating Decimal Fractions:
The decimal number with a finite number of digits after the decimal point is called a terminating decimal number.
Examples:
\( \frac{2}{5} = 0.4 \) and \( \frac{3}{8} = 0.375 \)
-
Recurring and Non-Terminating Decimal Fractions:
The decimal numbers with an infinitely repeating pattern of digits after the decimal point are called non-terminating and recurring decimal numbers.
Examples:
\( \frac{1}{3} = 0.333\ldots = 0.\overline{3} \) (3 repeats infinitely)
\( \frac{1}{6} = 0.166\ldots = 0.1\overline{6} \) (6 repeats infinitely)
\( \frac{22}{7} = 3.142857142857\ldots = 3.\overline{142857} \) (the pattern 142857 repeats infinitely)
5. What are irrational numbers in terms of their decimal representation?
Decimal numbers that do not repeat a pattern of digits after the decimal point continue indefinitely without terminating.
Non-terminating and non-recurring decimal numbers are known as irrational numbers.
Examples:
- \( \pi = 3.1415926535897932\ldots \)
- \( e = 2.71828182845904\ldots \)
- \( \sqrt{2} = 1.41421356237309\ldots \)
Note:
- \( e = 2.7182\ldots \) is called Euler's Number.
- Rational number + Irrational number = Irrational number.
- Rational number (≠ 0) × Irrational number = Irrational number.
- The product of two irrational numbers can be either rational or irrational, depending on the numbers involved.
6. Explain the concept of radicals and radicands.
If \( n \) is a positive integer greater than 1 and \( a \) is a real number, then any real number \( x \) such that \( x^{n} = a \) is called (radical) the \( n^{th} \) root of \( a \), and in symbols is written as:
\( x^{n} = a \)
\( \left[ x^{n} \right]^{\frac{1}{n}} = \left[ a \right]^{\frac{1}{n}} \)
\( x = a^{\frac{1}{n}} \)
\( x = \sqrt[n]{a} \)
In the radical \( \sqrt[n]{a} \), the symbol \( \sqrt{} \) is called the radical sign, \( n \) is called the index of the radical and the real number \( a \) under the radical sign is called the radicand or base.
7. Define surd.
An irrational radical with rational radicand is called a surd.
Examples of surds:
- \( \sqrt{5} \) (does not give a whole number)
- \( \sqrt{3}, \quad \sqrt[3]{7} \)
Not surds:
- \( \sqrt{9} \) (simplifies to 3, a whole number)
- \( \sqrt{\pi}, \quad \sqrt{e} \)
Note: Every surd is an irrational number, but not every irrational number is a surd (e.g., \( \sqrt{\pi} \) is irrational but not a surd) and the product of two conjugate surds is a rational number.
8. Monomial Surd
A surd which contains a single term.
Examples: \( \sqrt{2}, \quad \sqrt{3} \)
9. Binomial Surd
A surd which contains sum of two monomial surds or sum of a monomial surd and a rational number.
Examples: \( \sqrt{2} + \sqrt{7}, \quad \sqrt{2} + 5 \)
10. Conjugate Surd
Conjugate surd of \( \sqrt{a} + \sqrt{b} \) is defined as \( \sqrt{a} - \sqrt{b} \).
11. What are the additive properties of real numbers?
| Name of the Property | ∀ a, b, c ∈ ℝ | Examples |
|---|---|---|
| Closure | \( a + b \in \mathbb{R} \) | \( 2 + 3 = 5 \in \mathbb{R} \) |
| Commutative | \( a + b = b + a \) |
\( 2 + 5 = 5 + 2 \) \( 7 = 7 \) |
| Associative | \( a + (b + c) = (a + b) + c \) |
\( 2 + (3 + 5) = (2 + 3) + 5 \) \( 2 + 8 = 5 + 5 \) \( 10 = 10 \) |
| Identity | \( a + 0 = a = 0 + a \) | \( 5 + 0 = 5 = 0 + 5 \) |
| Inverse | \( a + (-a) = (-a) + a = 0 \) | \( 6 + (-6) = (-6) + 6 = 0 \) |
12. What are the multiplicative properties of real numbers?
| Name of the Property | ∀ a, b, c ∈ ℝ | Examples |
|---|---|---|
| Closure | \( ab \in \mathbb{R} \) | \( 2 \times 5 = 10 \in \mathbb{R} \) |
| Commutative | \( ab = ba \) |
\( 2 \times 5 = 5 \times 2 \) \( 10 = 10 \) |
| Associative | \( a(bc) = (ab)c \) |
\( 2 \times (3 \times 5) = (2 \times 3) \times 5 \) \( 2 \times 15 = 6 \times 5 \) \( 30 = 30 \) |
| Identity | \( a \times 1 = a = 1 \times a \) | \( 5 \times 1 = 5 = 1 \times 5 \) |
| Inverse | \( a \times \frac{1}{a} = \frac{1}{a} \times a = 1 \) | \( 6 \times \frac{1}{6} = \frac{1}{6} \times 6 = 1 \) |
Note:
- \( 0 \) and \( 1 \) are the additive and multiplicative identities of real numbers, respectively.
- \( 0 \in \mathbb{R} \) has no multiplicative inverse.
13. What are the distributive properties of real numbers?
| Property | Mathematical Expression |
|---|---|
| Left Distributive Property of Multiplication over Addition | \( a(b + c) = ab + ac \) |
| Left Distributive Property of Multiplication over Subtraction | \( a(b - c) = ab - ac \) |
| Right Distributive Property of Multiplication over Addition | \( (a + b)c = ac + bc \) |
| Right Distributive Property of Multiplication over Subtraction | \( (a - b)c = ac - bc \) |
14. What are the properties of equality of real numbers?
| No. | Property Name | Mathematical Expression |
|---|---|---|
| i | Reflexive Property | \( \forall a \in \mathbb{R}, \quad a = a \) |
| ii | Symmetric Property |
\( \forall a,b \in \mathbb{R}, \) \( a = b \Rightarrow b = a \) |
| iii | Transitive Property |
\( \forall a,b,c \in \mathbb{R}, \) \( a = b \land b = c \Rightarrow a = c \) |
| iv | Additive Property |
\( \forall a,b,c \in \mathbb{R}, \) \( a = b \Rightarrow a + c = b + c \) |
| v | Multiplicative Property |
\( \forall a,b,c \in \mathbb{R}, \) \( a = b \Rightarrow ac = bc \) |
| vi | Cancellation Property w.r.t Addition |
\( \forall a,b,c \in \mathbb{R}, \) \( a + c = b + c \Rightarrow a = b \) |
| vii | Cancellation Property w.r.t Multiplication |
\( \forall a,b,c \in \mathbb{R}, \) \( ac = bc \Rightarrow a = b \) |
15. State and explain the Multiplicative Property of order with examples.
| No. | Property Name | Mathematical Expression |
|---|---|---|
| i | Trichotomy Property |
\( \forall a,b \in \mathbb{R}, \) Either \( a = b \) or \( a > b \) or \( a < b \) |
| ii | Transitive Property |
\( \forall a,b,c \in \mathbb{R}, \) - \( a > b \land b > c \Rightarrow a > c \) - \( a < b \land b < c \Rightarrow a < c \) |
| iii | Additive Property |
\( \forall a,b,c \in \mathbb{R}, \) - \( a > b \Rightarrow a + c > b + c \) - \( a < b \Rightarrow a + c < b + c \) |
| iv | Multiplicative Property |
\( \forall a,b,c \in \mathbb{R}, \) - \( a > b \Rightarrow ac > bc \) if \( c > 0 \) - \( a < b \Rightarrow ac < bc \) if \( c > 0 \) - \( a > b \Rightarrow ac < bc \) if \( c < 0 \) - \( a < b \Rightarrow ac > bc \) if \( c < 0 \) - \( a > b \land c > d \Rightarrow ac > bd \) - \( a < b \land c < d \Rightarrow ac < bd \) |
| v | Division Property |
\( \forall a,b,c \in \mathbb{R}, \) - \( a > b \Rightarrow \frac{a}{c} > \frac{b}{c} \) if \( c > 0 \) - \( a < b \Rightarrow \frac{a}{c} < \frac{b}{c} \) if \( c > 0 \) - \( a > b \Rightarrow \frac{a}{c} < \frac{b}{c} \) if \( c < 0 \) - \( a < b \Rightarrow \frac{a}{c} > \frac{b}{c} \) if \( c < 0 \) |
| vi | Reciprocal Property |
\( \forall a,b \in \mathbb{R} \) and have same sign - \( a > b \Rightarrow \frac{1}{a} < \frac{1}{b} \) - \( a < b \Rightarrow \frac{1}{a} > \frac{1}{b} \) |
16. Write the Laws of Radicals and Indices.
| Laws of Radical | Laws of Indices |
|---|---|
| (i) \( \sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b} \) | (i) \( a^{m} \cdot a^{n} = a^{m + n} \) |
| (ii) \( \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \) | (ii) \( \left( a^{m} \right)^{n} = a^{mn} \) |
| (iii) \( \sqrt[n]{a^{m}} = \left( \sqrt[n]{a} \right)^{m} \) | (iii) \( (ab)^{n} = a^{n}b^{n} \) |
| (iv) \( \left( \sqrt[n]{a} \right)^{n} = \left( a^{\frac{1}{n}} \right)^{n} = a \) | (iv) \( \left( \frac{a}{b} \right)^{n} = \frac{a^{n}}{b^{n}} \) |
| (v) \( \frac{a^{m}}{a^{n}} = a^{m - n} \) | |
| (vi) \( a^{0} = 1 \) |
17. Is 0 a rational number? Explain.
Yes, 0 is a rational number because it can be written in the form \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \).
Examples: \( \frac{0}{1}, \frac{0}{2}, \frac{0}{3} \), etc., are valid rational numbers.
Since 0 divided by any nonzero integer is always 0, it satisfies the definition of a rational number.