Unit 11: Loci and Construction
Class 9 Mathematics | Punjab Curriculum and Textbook Board Syllabus 2025
1. Define Locus.
A locus (plural loci) is a set of points that follow a given rule. In geometry, loci help define the positions of points relative to one another or to geometric figures.
For example, if a point moves so that it always stays 5 cm away from a fixed point, then the locus of that moving point is a circle with a radius of 5 cm, centered at the fixed point.
2. Write types of triangles.
Types of Triangles (by sides):
- Scalene triangle: All sides are of different lengths.
- Isosceles triangle: Two sides are of equal length.
- Equilateral triangle: All sides are of equal length.
Types of Triangles (by angles):
- Acute-angled triangle: All angles measure less than \(90^\circ\).
- Obtuse-angled triangle: One angle measures greater than \(90^\circ\).
- Right-angled triangle: One angle measures exactly \(90^\circ\).
Note:
- An equilateral triangle is acute angled triangle.
- A right-angled triangle cannot be equilateral.
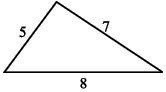
3. What is the Triangle Inequality Theorem?
The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
For example, for a triangle with sides 5 cm, 7 cm, and 8 cm:
\(5 + 7 > 8\)
\(5 + 8 > 7\)
\(7 + 8 > 5\)
So, the triangle satisfies the triangle inequality rule.
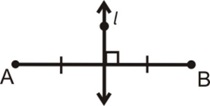
4. Define perpendicular bisector.
A perpendicular bisector is a line that intersects a line segment at right angle and divides it into two equal parts.
In other words, it intersects the line segment at its midpoint and forms right angles \(90^\circ\) with it.
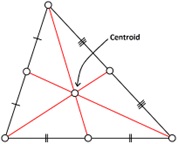
5. Define median of a triangle.
A median of a triangle is a line segment that joins a vertex to the midpoint of the side that is opposite to that vertex.
6. What is centroid?
The point of concurrency of the medians of a triangle is called centroid of the triangle.
7. What is a point of concurrency?
A point of concurrency is the single point where three or more lines, rays, or line segments intersect or meet in a geometric figure.
8. What is circumcentre?
The point of concurrency of perpendicular bisector of the sides of a triangle is called circumcentre.
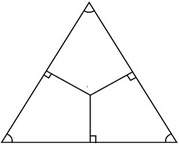
9. What is an angle bisector of a triangle?
An angle bisector of a triangle is a line or ray that divides an angle into two equal parts, creating two smaller angles that are congruent (each having half the measure of the original angle).
10. What is an altitude of a triangle?
Altitude is a ray drawn perpendicular from a vertex to the opposite side of the triangle.
There are three altitudes of the triangle which meet at a single point, i.e. the altitudes of a triangle are concurrent.

11. What is orthocentre?
The point of concurrency of the altitudes of the triangle is called the orthocentre of the triangle.
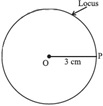
12. Define circle as a locus.
The locus of a point whose distance is constant from a fixed point is called a circle.
For example, the locus of a point \( P \) whose distance is \( 3\ cm \) from a fixed point \( O \) is a circle of radius \( 3\ cm \) and centre at \( O \).
13. Define parallel lines as a locus.
The locus of a point whose distance from a fixed line is constant are parallel lines (i.e. \( l \) and \( m \)).
For example, the locus of a point \( P \) whose distance is \( 2.5\ cm \) from a fixed line \( AB \) forms two parallel lines.
The locus of points equidistant from a line segment forms a long oval-like shape around the line — like a sausage or a running track.

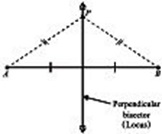
14. Define perpendicular bisector as a locus.
The locus of a point whose distance from two fixed points is constant is called a perpendicular bisector.
For example, the locus of a point \( P \) equidistant from \( A \) and \( B \) is the perpendicular bisector of line segment \( AB \).
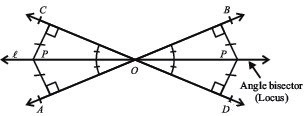
15. Define angle bisector as a locus.
The locus of a point whose distance is constant from two intersecting lines is called an angle bisector.
For example, the locus of a point \( P \) equidistant from lines \( AB \) and \( CD \) (intersecting at \( O \)) is the angle bisector \( l \) of \( \angle AOC \) and \( \angle BOD \).