Unit 8: Logic
Class 9 Mathematics | Punjab Curriculum and Textbook Board Syllabus 2025
1. What is logic?
Logic is a systematic method of reasoning that enables us to interpret the meanings of statements, examine their truth, and deduce new information from existing facts.
It plays a key role in problem-solving and decision-making.
Note: The study of logic begins with understanding a statement, which is a sentence that is either true or false, but not both.
2. What is inductive reasoning (induction)?
Inductive reasoning is when we make a general conclusion from repeated observations or experiences.
Example: A person receives a penicillin injection once or twice and experiences a reaction. He concludes that he is allergic to penicillin.
3. What is deductive reasoning (deduction)?
Deductive reasoning is when we draw a conclusion from already known or accepted facts.
Example: All men are mortal. We are men. So, we are mortal.
4. What is a statement?
A statement is a sentence or mathematical expression that is either true or false, but not both.
Example: The equation \( a = b \) is a statement, it can either be true or false, depending on the values of \( a \) and \( b \).
Note: We can think of a mathematical statement as a unit of information that is either accurate or inaccurate.
5. Give examples of true and false mathematical statements.
Examples of true statements:
- For a non-zero real number \( x \) and integers \( m \) and \( n \), we have: \( x^{m} \times x^{n} = x^{m + n} \)
- The sum of the measures of the interior angles of a triangle is \( 180^\circ \)
- The circumference of a circle with radius \( r \) is \( 2\pi r \)
- \( Q \subseteq R \) (The set of rational numbers is a subset of the set of real numbers)
Examples of false statements:
- \( 3 + 4 = 8 \)
- \( Z \subseteq W \)
- All isosceles triangles are equilateral triangles
- Between any two real numbers, there is no real number
6. How do we represent statements and logical operations in symbols?
The letters \( p \), \( q \) etc., are used to denote statements. A brief list of commonly used logical symbols is given below:
| Symbol | How to be read | Symbolic Expression | How to be read |
|---|---|---|---|
| \( \sim \) | Not | \( \sim p \) | Not \( p \), negation of \( p \) |
| \( \land \) | And | \( p \land q \) | \( p \) and \( q \) |
| \( \vee \) | Or | \( p \vee q \) | \( p \) or \( q \) |
| \( \rightarrow \) | If... then..., implies | \( p \rightarrow q \) | If \( p \) then \( q \), \( p \) implies \( q \) |
| \( \leftrightarrow \) | if and only if, Is equivalent to | \( p \leftrightarrow q \) | \( p \) if and only if \( q \), \( p \) is equivalent to \( q \) |
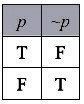
7. What is negation?
If \( p \) is any statement, its negation is denoted by \( \sim p \), read as "not \( p \)".
It follows from this definition that:
- If \( p \) is true, then \( \sim p \) is false.
- If \( p \) is false, then \( \sim p \) is true.
This relationship is shown in Truth Table.
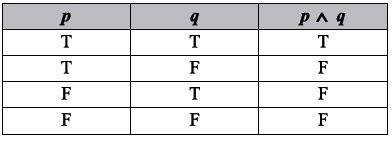
8. What is conjunction?
The conjunction of two statements \( p \) and \( q \) is symbolically written as \( p \land q \) (read as "\( p \) and \( q \)").
A conjunction is considered to be true only if both statements are true.
This relationship is shown in Truth Table.
9. Determine whether the following conjunctions are true or false.
- Lahore is the capital of the Punjab and Quetta is the capital of Balochistan.
- 4 < 5 and 8 < 10
- 2 + 2 = 3 and 6 + 6 = 10
Solution:
(i) is true (both parts are true).
(ii) is true (both inequalities are true).
(iii) is false (both mathematical statements are false).
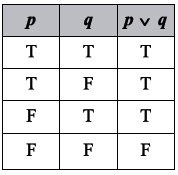
10. What is a disjunction?
The disjunction of statements \( p \) and \( q \) is symbolically written as \( p \vee q \) (read as "\( p \) or \( q \)").
A disjunction is true when at least one of the statements is true. It is false only when both statements are false.
This relationship is shown in Truth Table.
11. Determine the truth value of the disjunction: "10 is a positive integer or 0 is a rational number."
Both statements are true, so the disjunction is true.
12. Determine the truth value of the disjunction: "A triangle can have two right angles or Lahore is the capital of Sindh."
Both statements are false, so the disjunction is false.
13. What is an implication or conditional statement?
A compound statement of the form "if \( p \) then \( q \)" (symbolically written as \( p \rightarrow q \)) is called a conditional or an implication. It may also be read as "\( p \) implies \( q \)".
- \( p \) is called the antecedent or hypothesis.
- \( q \) is called the consequent or conclusion.
A conditional statement \( p \rightarrow q \) is considered to be:
- False only when the antecedent \( p \) is true and the consequent \( q \) is false.
- True in all other cases.

14. Explain implication with a real-life situation.
Statement: If person A lives in Lahore, then he lives in Pakistan.
Let us examine all possibilities:
- If A does live in Lahore and does live in Pakistan → the statement is true.
- If A lives in Lahore but not in Pakistan → the statement is false (this is the only false case).
- If A does not live in Lahore but lives in Pakistan → we cannot say the statement is false; it's considered true.
- If A does not live in Lahore and does not live in Pakistan → we still cannot reject the implication; it's regarded as true.
15. What is a biconditional or equivalence?
The statement \( p \rightarrow q \land q \rightarrow p \) is shortly written as \( p \leftrightarrow q \) and is called the biconditional or equivalence. It is read as "\( p \) if and only if \( q \)".
From the truth table, it appears that \( p \leftrightarrow q \) is true only when both statements \( p \) and \( q \) are true or both are false.
16. What are the conditionals related to a given conditional statement, and how do their truth values compare?
Let \( p \) and \( q \) be statements, and let \( p \rightarrow q \) be a given conditional. Then:
- The statement \( q \rightarrow p \) is called the converse of \( p \rightarrow q \).
- The statement \( \sim p \rightarrow \sim q \) is called the inverse of \( p \rightarrow q \).
- The statement \( \sim q \rightarrow \sim p \) is called the contrapositive of \( p \rightarrow q \).
The truth values of the Conditional, Converse, Inverse, and Contrapositive are shown in the truth table:
| \( p \) | \( q \) | \( \sim p \) | \( \sim q \) | \( p \rightarrow q \) | \( q \rightarrow p \) | \( \sim p \rightarrow \sim q \) | \( \sim q \rightarrow \sim p \) |
|---|---|---|---|---|---|---|---|
| \( T \) | \( T \) | \( F \) | \( F \) | \( T \) | \( T \) | \( T \) | \( T \) |
| \( T \) | \( F \) | \( F \) | \( T \) | \( F \) | \( T \) | \( T \) | \( F \) |
| \( F \) | \( T \) | \( T \) | \( F \) | \( T \) | \( F \) | \( F \) | \( T \) |
| \( F \) | \( F \) | \( T \) | \( T \) | \( T \) | \( T \) | \( T \) | \( T \) |
17. What can be concluded from this truth table of Converse, Inverse, Contrapositive?
- A conditional and its contrapositive are logically equivalent.
- The converse and inverse of a conditional are logically equivalent to each other.
18. How do you construct the truth table for \( \left[ \left( p \rightarrow q \right) \land p \right] \) and \( \left[ \left( p \rightarrow q \right) \land p \right] \rightarrow q \)?
| \( p \) | \( q \) | \( p \rightarrow q \) | \( (p \rightarrow q) \land p \) | \( \left[(p \rightarrow q) \land p\right] \rightarrow q \) |
|---|---|---|---|---|
| \( T \) | \( T \) | \( T \) | \( T \) | \( T \) |
| \( T \) | \( F \) | \( F \) | \( F \) | \( T \) |
| \( F \) | \( T \) | \( T \) | \( F \) | \( T \) |
| \( F \) | \( F \) | \( T \) | \( F \) | \( T \) |
19. How can we prove that the empty set \( \phi \) is a subset of any set \( A \)?
Let \( U \) be the universal set. Consider the conditional:
\( \forall x \in U, \quad x \in \phi \rightarrow x \in A \)
The antecedent of this conditional is false because no \( x \in U \) is a member of \( \phi \). Hence, the conditional is true.
20. What is a Mathematical Proof?
In daily life, we often need to prove our claims using solid evidence.
Example 1: If a student named Fayyaz comes home late, his father may doubt he attended school. Just saying "I went to school" is not enough—he needs proof, like:
- The school attendance register, or
- CCTV footage from the school.
Example 2: If your mobile phone breaks down and it's under warranty, the company will ask for a warranty card as proof before fixing it.
21. Define Mathematical Proof.
In mathematics, a proof is a step-by-step logical explanation that shows a statement is true.
It is like evidence that supports a mathematical claim.
Note:
If \( x \) is an odd integer, then it can be expressed in the form:
\( x = 2k + 1, \quad \text{for some } k \in \mathbb{Z} \)
If \( x \) is an even integer, then it can be expressed in the form:
\( x = 2k, \quad \text{for some } k \in \mathbb{Z} \)
22. Prove the following mathematical statements:
- If \( x \) is an odd integer, then \( x^2 \) is also an odd integer.
- The sum of two odd numbers is an even number.
(a) Solution:
Let \( x \) be an odd integer. By definition, an odd number can be written as:
\( x = 2k + 1, \quad \text{where } k \in \mathbb{Z} \)
Now taking square both sides:
\( x^{2} = (2k + 1)^{2} \)
\( x^{2} = (2k)^{2} + 2(2k)(1) + (1)^{2} \)
\( x^{2} = 4k² + 4k + 1 \)
\( x^{2} = 2(2k² + 2k) + 1 \)
Let \( m = 2k² + 2k \), which is an integer (since \( k \in \mathbb{Z} \)), so:
\( x^{2} = 2m + 1 \)
This is the standard form of an odd number. Therefore, \( x^{2} \) is an odd integer, by definition.
(b) Solution:
Let \( x \) and \( y \) be odd integers. By definition:
\( x = 2k + 1 \quad \text{where } k \in \mathbb{Z} \)
and \( y = 2n + 1, \quad \text{where } n \in \mathbb{Z} \)
Now adding both:
\( x + y = (2k + 1) + (2n + 1) \)
\( x + y = 2k + 2n + 2 \)
\( x + y = 2(k + n + 1) \)
Let \( m = k + n + 1 \), which is an integer.
So:
\( x + y = 2m \)
This is the standard form of an even number. Therefore, the sum of two odd integers is an even integer, by definition.
23. Prove that for any two non-empty sets \( A \) and \( B \):
- \( (A \cup B)' = A' \cap B' \)
- \( (A \cap B)' = A' \cup B' \)
(i) Solution:
Let \( x \in (A \cup B)' \)
\( \Rightarrow x \notin (A \cup B) \)
\( \Rightarrow x \notin A \text{ and } x \notin B \)
\( \Rightarrow x \in A' \text{ and } x \in B' \)
\( \Rightarrow x \in A' \cap B' \)
Since \( x \in (A \cup B)' \) was arbitrary, we conclude:
\( (A \cup B)' \subseteq A' \cap B' \quad \ldots (i) \)
Now suppose \( y \in A' \cap B' \)
\( \Rightarrow y \in A' \text{ and } y \in B' \)
\( \Rightarrow y \notin A \text{ and } y \notin B \)
\( \Rightarrow y \notin (A \cup B) \)
\( \Rightarrow y \in (A \cup B)' \)
Thus:
\( A' \cap B' \subseteq (A \cup B)' \quad \ldots (ii) \)
From \( (i) \) and \( (ii) \), we conclude:
\( (A \cup B)' = A' \cap B' \)
(ii) Solution:
Let \( x \in (A \cap B)' \)
\( \Rightarrow x \notin (A \cap B) \)
\( \Rightarrow x \notin A \text{ or } x \notin B \)
\( \Rightarrow x \in A' \text{ or } x \in B' \)
\( \Rightarrow x \in A' \cup B' \)
Since \( x \in (A \cap B)' \) was arbitrary, we conclude:
\( (A \cap B)' \subseteq A' \cup B' \quad \ldots (i) \)
Now suppose \( y \in A' \cup B' \)
\( \Rightarrow y \in A' \text{ or } y \in B' \)
\( \Rightarrow y \notin A \text{ or } y \notin B \)
\( \Rightarrow y \notin (A \cap B) \)
\( \Rightarrow y \in (A \cap B)' \)
Thus:
\( A' \cup B' \subseteq (A \cap B)' \quad \ldots (ii) \)
From \( (i) \) and \( (ii) \), we conclude:
\( (A \cap B)' = A' \cup B' \)
24. What is a theorem in mathematics?
A theorem is a mathematical statement that has been proved to be true using logical steps based on previously accepted facts, definitions, or other theorems.
25. What is the angle sum of a quadrilateral?
The sum of interior angles of any quadrilateral is \( 360^\circ \).
26. What is the Fundamental Theorem of Arithmetic?
Every integer greater than 1 can be uniquely written as a product of prime numbers, ignoring the order of the factors. OR
Every whole number greater than 1 can be written as a product of prime numbers, in only one way (ignoring order).
27. What is Fermat's Last Theorem?
There are no positive numbers \( a, b, c \) such that
\( a^{n} + b^{n} = c^{n} \text{ for any } n > 2. \)
This statement was made by Pierre Fermat, a French mathematician from the 17th century.
28. What is a conjecture?
A conjecture is a mathematical statement that is believed to be true, based on observations, but not yet proven.
- If a conjecture is proven, it becomes a theorem.
- If it is disproved, it is considered false.
29. What is Goldbach's Conjecture?
The Goldbach Conjecture says: Every even number greater than 2 is the sum of two prime numbers. For example,
\( 4 = 2 + 2 \)
\( 6 = 3 + 3 \)
\( 12 = 5 + 7 \)
Although no one has found an even number that violates this, the conjecture has not yet been proved. It remains one of the oldest unsolved problems in mathematics.
30. What is an axiom?
An axiom is a basic mathematical fact that is accepted as true without proof. It forms the foundation of mathematics.
Example: Through a point, infinitely many lines can pass. We accept it as true based on intuition and experience.
31. What are some examples of axioms?
- Euclid's Axiom: A straight line can be drawn between any two points.
- Peano's Axiom: Every natural number has a successor.
- Axiom of Extensionality: Two sets are equal if they have the same elements.
- Axiom of Power Set: Every set has a set of all its subsets.
32. What is the difference between an axiom and a postulate?
Both are assumed to be true without proof.
- Axioms apply to all branches of mathematics.
- Postulates are used especially in geometry.
33. What is a deductive proof?
A deductive proof is a method of proving a statement by using logical reasoning from facts that are already known to be true. For example,
Premise 1: All human beings need to breathe to live.
Premise 2: Ahmad is a human.
Conclusion: Therefore, Ahmad needs to breathe to live.
34. Write the converse, inverse, and contrapositive of the following conditionals:
- \( \sim p \rightarrow q \)
- \( q \rightarrow p \)
- \( \sim p \rightarrow \sim q \)
- \( \sim q \rightarrow \sim p \)
| Conditional | Converse | Inverse | Contrapositive |
|---|---|---|---|
| \( \sim p \rightarrow q \) | \( q \rightarrow \sim p \) | \( p \rightarrow \sim q \) | \( \sim q \rightarrow p \) |
| \( q \rightarrow p \) | \( p \rightarrow q \) | \( \sim q \rightarrow \sim p \) | \( \sim p \rightarrow \sim q \) |
| \( \sim p \rightarrow \sim q \) | \( \sim q \rightarrow \sim p \) | \( p \rightarrow q \) | \( q \rightarrow p \) |
| \( \sim q \rightarrow \sim p \) | \( \sim p \rightarrow \sim q \) | \( q \rightarrow p \) | \( p \rightarrow q \) |
35. Differentiate between a mathematical statement and its proof. Give two examples.
| Mathematical Statement | Mathematical Proof |
|---|---|
|
A mathematical statement is a sentence or mathematical expression that is either true or false but not both. |
A proof is a logical explanation that verifies a statement using definitions, axioms, known theorems, or logical reasoning. |
|
(i) If \( x \) is an odd integer, then \( x^{2} \) is also an odd integer. (ii) The sum of two odd numbers is an even number. |
(i) If \( x = 2k + 1 \Rightarrow x^{2} = 2m + 1 \) → Odd (proved using algebra). (ii) If \( x = 2k + 1, y = 2n + 1 \Rightarrow x + y = 2m \) → Even (proved using identities). |
36. Difference between an Axiom and a Theorem.
| Axiom | Theorem |
|---|---|
|
An axiom is a mathematical statement accepted without proof. It is based on basic facts or everyday experience and forms the foundation of further reasoning. |
A theorem is a mathematical statement that has been proven true using axioms, previously known theorems, and logical steps. |
|
(i) Through a given point, infinitely many lines can pass. (ii) Euclid's Axiom: A straight line can be drawn between any two points. |
(i) The sum of interior angles of a quadrilateral is 360°. (ii) Fundamental Theorem of Arithmetic: Every integer greater than 1 can be expressed uniquely as a product of primes. |
37. What is the importance of logical reasoning in mathematical proofs? Give an example to illustrate your point.
Logical reasoning is essential in mathematics because it allows us to prove or disprove statements using facts, definitions, and structured thinking. Without logical reasoning, we cannot be certain whether a mathematical statement is valid.
Consider this deductive reasoning:
- Premise 1: All human beings need to breathe to live.
- Premise 2: Ahmad is a human.
- Conclusion: Therefore, Ahmad needs to breathe to live.
This same type of reasoning is used in mathematical deductive proofs. For example, in algebra, we use identities and rules to show that both sides of an equation are equal through step-by-step logic. This ensures the result is always true if the premises are true.
38. Identify: Axiom, Conjecture, or Theorem.
- There is exactly one straight line through any two points.
- Every even number greater than 2 can be written as the sum of two primes.
- The sum of the angles in a triangle is \( 180^\circ \)
| Statement | Type | Reasoning |
|---|---|---|
| (i) There is exactly one straight line through any two points. | Axiom | This is a basic assumption in Euclidean geometry, accepted without proof. |
| (ii) Every even number greater than 2 can be written as the sum of two primes. | Conjecture | This is the Goldbach Conjecture, believed to be true but not yet proven. |
| (iii) The sum of the angles in a triangle is \( 180^\circ \) | Theorem | This is a proven result in Euclidean geometry, based on axioms and logical reasoning. |